The Grand Patchwork

 

Running head: REACHING THE GOOD: A NEW UNDERSTANDING OF PLATO

 

 

 

 

 

 

 

Reaching the Good: A New Understanding of Plato’s Allegory of the Cave and Plotting the Elusive Divided Line

Sandra Kroeker

Revised from a term paper for partial credit in Philosophy of Ethics at

Brock University

Dr. Calvin Hayes

November 11, 2010

Revised 2015 and presented for the Society for the Advancement of Paraphilosophical Studies

 

 

 

 

 

 

 

Reaching the Good: A New Understanding of Plato’s Allegory of the Cave and Plotting the Divided Line

Allegory of the Cave

            Plato likens people to slaves or prisoners shackled inside a cave who have been there since birth and can only look forward onto the cave wall; as their necks are also braced. Behind them is a burning fire and between the prisoners and the fire is a puppet show as well as people holding objects so that the prisoners are only seeing the shadows of these objects on the wall. One prisoner escapes and ends up out of the cave and into the sunlight. His eyes hurt from the brightness and need to adjust. Once adjusted, he sees the world in all its glory including the sun. This, according to Plato, is the state of the world and refers to it as a “meaningless illusion” (Johnson & Reath, 2007, p. 56; Cornford, 1965, p229). Plato states that

[W]e must conclude that education is not what it is said to be by some…the entire soul

 must be turned away from this changing world until its eye can bear to contemplate

reality and that supreme splendour which we have called the Good…There is nothing

wrong with… the power of vision, but it has been forced into the service of evil, so that

the keener its sight, the more harm it works.” (Cornford, 1965, pp. 232-233)

Plato is saying that persons are following or living a life that is based on a ’meaningless illusion; influenced by those who are leading us astray from true reality. He believes we have not been educated properly in regard to finding the truth, which is the Good (Johnson & Reath, 2007). This paper will analyze what Plato means by this statement. Plato seems to say that everything we are taught is based in falsehood and lies. This seems a little harsh to me, but there may be a kernel of truth behind what he is saying. However, instead of saying that everything we have been taught is based on a ‘meaningless illusion,’ I will instead say half-truths and misconceptions. Therefore, this paper will endeavour to explore Plato’s harsh accusation.  

This paper will first analyze the Allegory of the Cave and then the Divided Line. The first section will unpack what each aspect in the Cave analogy represents (up to seeing the real world and the sun) and go deeper into what it means to say we have not been educated properly in regard to the truth. It was found that some knowledge has been taught (consciously or unwittingly) from ideologies that are half-truths or based on misconceptions. Our knowledge and curricula may need a little bolstering to become more complete and representative. Concepts taught from a reductionistic and mechanistic ideology will be analyzed (half truths) and binaristic thinking and propaganda pontificated from some positions of power will also be examined (misconceptions). Suggestions for teaching more accurate and complete information will be discussed.

The second section turns its eye to Plato’s Divided Line analogy; the actual plotting of which has baffled philosophers and mathematicians for centuries. Mathematics, in particular secular mathematics, was found to be incomplete and in need of other approaches (which will be discussed) in order for it to be complete and more interesting to everyone; especially girls and women. This was determined through a revolutionary breakthrough in which this paper presents; a solution to a century old problem of how to plot/draw/depict Plato’s Divided Line.  This paper also explains how to travel along the Line to enlightenment (an understanding of the truth). I was born and raised in Canada; therefore my observations are from a western-influenced perspective. I am female and can relate to the disinterest of mathematics instilled in girls and women in Canada. Operational definitions for the purposes of this paper are:

Enlightenment: A road to the discovery of the truth or true reality (the Good).

Good: Truth; what Plato considers to be the true reality; one not many ‘see.’ It is

 the realm of intelligence. This reality is ontologically superior to the reality we see or act

 upon in everyday life.

Puppet People: Persons in positions of power who willingly or unwittingly relay

misleading information or information that is incomplete (based on half truths) that

ends up interpreted as whole truth or fact. These are the people that ‘force the power of

vision to service evil,’ rather than the Good.

The Obstacles

According to Plato, it is extremely difficult to attain the Good due to the obstacles presented in the analogy. It could be said that the shackles represent the body, and the neck brace, the idea that persons are only shown one viewpoint or opinion. Since the prisoners have been there since birth, they do not know any alternative to what they are shown. The images or shadows suggest that what the prisoners have been taught their entire lives is not the real, true way of attaining what Plato calls the Good.

In the Allegory of the Cave, the people behind the prisoners would be the biggest obstacle to finding the Good because they serve the fire and not the sun (a false “good” which represents the material world or materialism; the world in which we need to turn away from). It is this fire that is casting the false simulation of reality onto the cave wall. These ‘puppet people’ are carrying objects and putting on puppet shows for the prisoners to view on the cave wall. These objects represent the real objects in the material world (as opposed to their shadows). The puppet show could be likened to a film projected onto a screen (Johnson & Reath, 2007). A film does not display verisimilitude, or present a true reflection of reality: Thus, reinforcing the idea that the prisoners are being taught a ‘meaningless illusion.’ Even though the objects reflected are real, they are used as a distraction from the reality that lies outside of the cave and are located behind the prisoners where they cannot see them directly.

The cave passage would represent the long painful journey towards enlightenment and attaining the Good. Plato mentions that the prisoner who escapes is dragged out the cave by force (Johnson & Reath, 2007; Cornford, 1965). He is also forced to stand and turn his head. These events suggest that it is not an easy passage out of the cave.

When the freed prisoner reaches the entrance (or exit) of the cave, his eyes have to adjust because he has to unlearn and relearn everything he has ever been taught. This stage of deconstruction and reconstruction is the beginning of enlightenment and the first step towards glimpsing the Good. This is represented by the prisoner seeing the world in all its glory, including the sun itself. He is then compelled to return to the prisoners to free them and reveal that their reality is a mere illusion. Plato believes that once the Good has been attained or even glimpsed, that person should become a ‘Philosopher King’ and rule on earth (Personal communication, C. Hayes, October, 2010). However, because the prisoners are so used to their existence they laugh at him, do not believe what he says and some wish to kill him in response (Johnson & Reath, 2007). “How dare you suggest that everything I have come to know is a lie!?” (added by author for dramatic effect). This is what happens to those who challenge the status quo and go against popular opinion. Socrates is a prime example because he challenged popular opinion and was subsequently sentenced to death for corrupting the youth.

Some might say that it is unreasonable for the one who has become enlightened to go back into the dark cave to be ridiculed and martyred (Personal communication, C. Hayes, October, 2010). It could be that enlightenment itself comes with new sense of unselfishness and an altruistic duty to help others, much like Kierkegaard’s “imminent alterity” or “otherness” which refers to the idea that as one becomes more ethical; they feel the need to take others into consideration ahead of themselves (Stan, 2010). Piff, Dietze, Feinberg, Stancato and Keltner (2015) found that the feeling of awe is correlated with an increase in ethical behaviour and altruism. This phenomenon can also be found in the life of a Bodhisattva in the Buddhist tradition, as they have reached an enlightened state that compels them to vow to reincarnate to help others reach the state of Nirvana, at the expense of not enjoying Nirvana for themselves. Nirvana could be considered similar to Plato’s concept of the Good.

In summation, the existence in the cave represents existence in the material world or materialism and the fire represents the actual sun (Johnson & Reath, 2007). The journey up and out of the cave into the ‘real world’ represents intelligence or the path to enlightenment and the truth, which is the Good (Johnson & Reath, 2007). Intelligence, therefore, represents transcendence from the material realm to that of the ‘enlightened’ realm, which is considered more ontologically real than the material realm as it is the true reality. The obstacles between the material realm and reaching the Good are the teachings that divert a person away from the Good and towards the ‘meaningless illusion.’ But, what is this illusion?

The Illusion

Like Hinduism, which has a word for this illusion (maya) is similar to what Plato is trying to convey. More contemporary examples include Star Trek’s ‘Holo-deck’ or the material world as presented in the movie The Matrix (The Wachowskis, 1999). Much like how these pop culture references portray the world, Plato is trying to get across that the world we see or act upon is not the true reality and that there is more to life than what we are shown or taught. There are many distractions from enlightenment and attaining the Good. Going back to Socrates, he was led to the slaughter by those who wish to keep projecting the ‘meaningless illusion’ because he kept poking holes in it. There are those who enjoy the spoils of this illusion and do not wish to relinquish any power or control over the masses. This ultimately, is why Socrates was killed!

Similar to trends in science fiction, mystical sects also expound Plato’s belief in a higher reality and that we have been led astray by those in positions of power (as symbolized by the ‘puppet people’ behind the prisoners in the cave casting puppet shows onto the wall). For example Gnosticism believes that the ruler of the earth or the world system is not the real, true god, but an evil, jealous god. He is the fallen angel who wishes to be worshipped like the real true God (Meyer, 2005) and usurp God’s power by persuading humankind to worship him instead. He does this by distracting us from the Good and forcing our eye towards the illusion. This is what Gnosticism would say about what we are taught in the illusion and it helps explain the role of the ‘puppet people’. The Gospel of Philip states:

The rulers wanted to fool people, since they saw that people have a kinship

with what is truly good. They took the names of the good and assigned them

to what is not good; to fool people with names and link the names to what is not good…

For, they wished to take free people and enslave them forever. (Meyer, 2005,p. 52)

This is exactly what Plato is trying to say about education and the prisoners in the Allegory of the Cave.

There is a similar passage in the Gospel of Thomas 39 that states: “The Pharisees and the scholars have taken the keys of knowledge and have hidden them. They have not entered, nor have they allowed those who want to enter to do so” (Meyer, 2005, p.14). It is hard to accept that what we have come to know is based on misleading information and half-truths, but research in Gender Studies has done a great job in shattering the illusion of main stream, popular discourse.

Examples of Misleading Teachings and Half-Truths

First of all, I would like add that there are probably kernels of truth in all teachings. But, discourse masquerades as truth from positions of power and erroneous beliefs are perpetuated. Half truths are assumed to be whole truth. For example, a professor is in a position of power and what is taught affects the student’s world view and belief system (Alcoff, 1991-1992). Those who promote quantitative analysis in the social sciences are relaying only half truths, in which some students come to believe as the whole truth. Quantitative analysis in the social sciences can only be used to describe humanity, yet inferences about how and why are made to the entire population more often than using it for mere description. Only with the addition of qualitative analysis can inferences about how and why be made. This provides more representative results of the entire population.

Even though the social sciences know this, this type of research assumes (incorrectly) that stereotypes, or something that can be said about 67% of the population, can be inferred to 100% of the population and a lot of the time procedures are put in place that consistently privilege a certain group over another (Narayan & Harding, 2000; Plumwood, 1993). It has gotten a lot better since I did my Psychology degree, but stereotypes and a ‘majority rules’ attitude is still maintained and utilized to influence great decisions and procedural structures. For example, some universities still remain inaccessible to persons in wheelchairs, but I have seen an improvement in recent years and have noticed more ramps and elevators etc. However, a lot of the time the ramps are found to be too narrow or way too steep, especially in the winter and thought has not been taken in which direction the automatic doors open to be more conducive to wheelchair access (Personal communication, A. Nonymous, April, 2014). New problems arise in the process of integrating persons with disabilities because those who experience these exceptionalities are not including in the planning process (Rioux & Fraser, 2005). This problem is also prevalent in procedures for students with learning disabilities (Hibbs & Pothier, 2005). This added stress and complication is an excellent example of how the centre keeps re-centring itself; despite efforts to integrate. This is how the majority still has power over the outliers. Moreover, many decisions and procedures are formed on the basis of politics within the institution, rather than solid evidence. This is another way the centre keeps re-centring itself and change toward equity is slow or stagnant.

Another example of how the dominant ideology and status quo remains central is in the concept of cultural capital and concerted cultivation. Concerted cultivation is the idea that certain parenting styles from different classes can help or hinder a child’s success. A middle class parenting style is regimented and structured, implanting certain skills that happen to advantage middle class children in a school environment that perpetuates middle class ideals (Lareau, 2011). The concept of cultural capital explains how sitting still in a structured classroom is rewarded and the recipients of its success are generally middle class children who have been exposed to more situations that facilitate this behaviour (Bourdieu, 1986). This perpetuates class differences and children who had the opportunity to grow up in the middle class are more likely to succeed (Lareau, 2011; Bourdieu, 1986). Free play is important for developing self-corrective and peer facilitated learning (St. John, 2010). This is why it is important to expose children to both structured and unstructured play and school curricula is more likely to reward and utilize methods that promote structure; when both are important for learning (St John, 2010).      

Another example of teachings that are misleading or incomplete is in the field of social sciences and quantitative methodology because it masquerades as objective, when the truth is, it is not. Commonly held beliefs influence one’s research (Harding, 2007). It is false to think a human can study humanity objectively while also immersed in the human experience (Personal communication H. Hunt, 2008). The commonly held beliefs of the researcher are assumed to be fact because they are told by their professors who pontificate from positions of power (Alcoff, 1991-1992). For example, back when slavery existed in the United States, there used to be a ‘disease’ called Drapetomania used to explain why slaves would run away. This is now considered pseudoscientific but can be used as an example of how science can promote racism or favour certain groups. Unfortunately this type of thing happens in education and science. Perhaps teachings that the world is flat may have been a better example.

Many researchers doctor their findings to lead to a conclusion they want. Some even change their hypothesis after their experiment to match their findings so they can be published. Once published, these misleading findings are given a position of power and regarded as fact. Generations of people carry on, oblivious to the fact that they have been manipulated and taught misleading and incomplete theories and ideologies; a lot of it for the impetus of personal gain or hidden political agendas of power and money.

On the other side of research, qualitative research is also incomplete. Quantitative analysis needs qualitative analysis and vice versa to be complete or to gather more well rounded and more representative data. If only one method is supported and funded, results are not as representative as they can be because only a part of the picture is being studied and tested. Quantitative is only good for describing and needs to incorporate qualitative approaches to explain the how and why. In this way, it could be seen how only one side or part of the story is highlighted and more revered, when the greater picture is obscured. This is why I call quantitative or qualitative methodology on its own, a half-truth.

Girls are placed in one category and boys in another and are told they have to act in certain ways and are consequently bullied if they step slightly out of these boxes. It is not possible to put a fluid, dynamic subject into a categorical box and expect them to stay there or encompass all the characteristics ascribed to that box. Evidence for this can be found when deconstructing terms or trying to create a universal definition of any word. There is no universal definition of love, for example. I challenge you to define the concept of a woman that includes 100% of its population. Who decides that aggressiveness is only for those with a penis? How can we agree on conclusions and implement solutions if we cannot even agree on a simple definition? This is how common discourse masquerades as truth; it is part of our language, part of our curricula, part of our culture. It is written into our history books, our TV shows and seen all around us. There is a difference between what Plato calls a puppet show, and the truth. We are socialized at birth to believe a girl should act one way and a boy another. Is this truth? This is what Plato is trying to say. I apologize for dragging you forcefully out of the cave. Welcome to the quest for the Good.

There are erroneous biases imbedded in our language, which in turn create a skewed world view or belief system. An example of how language can create a skewed world view is thinking in binaries. The conflict or stanch opposition between variables in a binary is an illusion, yet we commonly believe them to be drastically different; making their reconciliation difficult. Rarely are we taught they can work together as complements and rarely are we given more than two options in a situation. I challenge you to think of a binary and not place a higher distinction on one variable in the pair over another. We subconsciously assume right is better than left, up is better than down, positive is better than negative, when in reality these are neutral distinctions. Therefore, in this way, our world views are influenced by our language. For example, taking a look at the binary pairs above, the word right comes with other meanings and connotations. Right is also associated with correct, leading to a subconscious bias toward right over left. Also, for the majority of people, their right hand is dominant, adding to the bias. Children who were left-handed used to be forced to use their right hand; some children’s left hands were tied to the backs of their chair in grade school. This bias became so extreme that children who were left-handed were said to be spawns of the devil. Therefore, it could be said that the erroneous belief that right is better than left can lead to erroneous conclusions and implications. The same can be said about up and down. If you are feeling up, you feel good, and if you are feeling down, you are not in the optimal state. Likewise with positive and negative: Positive means to add something or do something, whereas negative means to take away or to not do certain behaviours. Both are valuable, yet we only think of the positive as being good. Sometimes, not doing a certain thing is better than doing a certain thing (Lao-Tzu, as cited by Henricks, 1989). But, we have a bias towards action as opposed to inaction etc. etc. etc. To realize or understand that what has been taught since birth is merely an illusion is a painful and difficult task; one many would not accept. This is why the Philosopher King is punished, but also why the Philosopher King feels a duty to tell others about the truth.

Another example of a teaching that is misleading is reductionism. The assumption that the sum of the parts can equal the whole underlies many teachings. General Systems Theory provides evidence that radical reductionism is impossible in the physical realm because the sum of the parts can only equal the whole when there is absolutely zero communication between any of the parts in that system; this is physically impossible in the material realm (Von Bertalanffy, 1972). Think of your body as a system. Is it possible to survive if none of the parts communicated at all? However, many schools of thought are founded on this assumption; from Psychology/Neuropsychology to Genetics.

To demonstrate this point more clearly, in the field of genetics an assumption that the world is a giant machine underlies all teachings (Sheldrake, 1988). These are called mechanistic approaches. The ideology that the world is a living organism and the ideology that the world is a machine have competed since the time of Plato (Sheldrake, 1988). However, the only way to explain how the same cells and genes can develop into two different things (arms and legs have the same cells and genes) is to acknowledge that organisms and by extension, the earth must be more like an organism than a machine. For example, regeneration of tissue cannot be explained through mechanistic explanations and therefore lends itself more to organistic theories. Experiment: Cut a worm in half and see what happens; then break a computer in half and see what happens. As I was typing that last sentence, the word mechanistic was in the dictionary, but the program highlighted organistic. This shows how one is favoured over the other, even though the one has been falsified and the other not.

Different genes actually interact co-operatively to develop different parts and organs. “[D]ifferent parts do not develop independently in a rigidly predetermined way. Rather they respond and adjust to each other” (Driesch as cited by Sheldrake, 1988, p.80). Therefore, organisms differ from machines (Sheldrake, 1988) and parts develop in more of a correlation than a causal direction from geneà phoneme à environment, which is what is more commonly taught because the common belief is that environment cannot directly change or affect genes (Scarr & McCartney, 1983). I disagree with this because the environment or socialization can trigger certain dormant genes to become activated and certain repetitive behaviours can alter neural connections in the brain no matter the age of the person. Also, skin colour is determined by the amount of sun concentration, which eventually affected the genes. Those who believe the world is a machine and runs on chance use reductionistic and mechanistic explanations to explain all sorts of phenomena. How does a sunflower bloom from a seed? The answer: Because it is “genetically programmed to do so” or the information is encoded in its genes (Sheldrake, 1988). Yet, here we have learned that genes cannot explain everything.

The term ‘genetic programming’ is misleading because it conjures up the idea that living organisms are programmed machines, yet the idea of a programmer is never discussed, but the idea that there must be a programmer is more parsimonious. For example, imaging you live in the jungle and have never come in contact with other humans and as you are walking along a path you find a watch. The intricacies of the watch and how the parts work together must preclude a watchmaker and a purpose or reason for making the watch. Even though there is overwhelming evidence that the world and organisms are more like an organism, science and genetics is still taught from the assumption the world and organisms are more like a machine. This causes reductionistic and mechanistic teachings and explanations to be incomplete or misleading (Sheldrake, 1988). Many assume that if the majority believes it, it must be true. Well, sorry to break it to you, but seven billion people can be wrong! 

What Can We Do?

In order to break the illusion of incomplete or misleading teachings and unshackle ourselves from the cave wall we need to unlearn and relearn everything we have been taught. This is called Critical Theory. Take everything we see or hear with a grain of salt and think things over before coming to reactive conclusions. We could be good critical consumers of the information presented to us. Then we could teach this to others. Teaching and applying a mixed methods approach when doing research in the social sciences would be beneficial, as would laying out a school curriculum that is both structured and unstructured.  Recognizing when decisions and procedures are being made based on assumptions promoted by the status quo would also be beneficial. “It is a useful exercise…to examine how our culture has come to be defined and shaped in specific ways-to excavate the origins of our most celebrated rituals” (Jhally, 2013, p.327). Common discourse tells us how to be happy and we are told this happiness comes “through and about objects” (Jhally, 2013, p. 328).  Perhaps we can understand that this is a teaching that distracts us and leads us towards the ‘meaningless illusion.’ We also need alternatives to binaristic thinking to eliminate the development of erroneous and arbitrary hierarchies (Plumwood, 1993).  However, this is a very complicated suggestion in light of Plato because he believes in an ontological superior world and intelligence is this world. Aristotle, Democritus and others believe the opposite and think that the more one goes in depth into organisms, to cells etc., the more real the realms become (Sheldrake, 1988). Both of these ideologies are apt, but both are incomplete without the other. There is an interaction or correlation between the worlds that makes both necessary; even though they perform different functions. A healthy balance between the guidelines of too much and too little would be optimal.

There is a travel or ‘progress’ along the path towards the Good, but it goes in all directions equally. Humans tend to assume ascension. Travelling along the path to the Good is not a linear concept, but human minds project onto it what they want to see or what they understand. I see it more like a correlation or an interaction; like a breath; not a linear ascent. I therefore disagree, in a way, with the ontological superiority of one realm over another when both are important for different reasons at different times. For example, it would asinine to say that it is better to breathe in than to breathe out. Both are equally necessary for growth and survival, just like reason and emotion should be considered equally valid human experiences (Kroeker, 2008). This extra stage of evaluation is what causes errors and misconceptions. Can it be possible to see the intelligible world and the material world as equal but different?

In conclusion, Plato may be on to something when he says that “education is not what it is said to be” (Cornford, 1965, p.232).     

The Divided Line

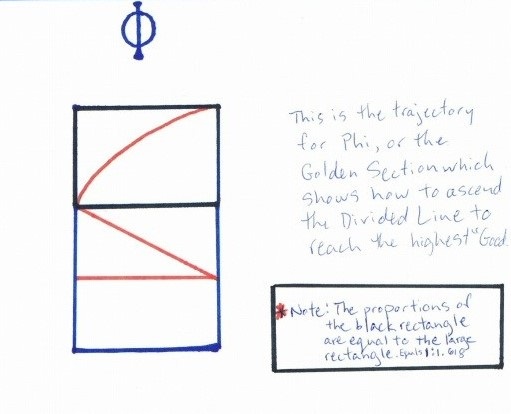
Even though I disagree with using the term ascend, Plato suggests how to ascend to the Good in his Divided Line. The Divided Line is a map, if you will, of the path to enlightenment. See Figure 1 for an amalgamation of the Allegory of the Cave and the concept of the Divided Line. The idea is that the line is to be divided into two unequal sections and then each section divided again using the same ratio (Balashov, 1994). The two major, unequal sections represent the material realm of the seen, or “being” from the world of the unseen, or the “intelligible” (Johnson & Reath, 2007, p. 54). It is important to note that the two major realms are ontologically unequal as the intelligible realm is considered superior to the visible/material realm. This makes sense because the physical world is subject to decay (as according to the second law of Thermodynamics), whereas the intelligible realm is not (first law of Thermodynamics). The ontological ranking is represented by the size of the ‘box’ in Figure 1, the larger the area, the more ontologically superior that realm is. It is also divided in half horizontally; the lower half is illusion and the upper half, truth (see the broken line in Figure 1).

The Allegory of the Cave is a metaphor used to help Plato explain concept of the Divided Line. In the Divided Line, the ruler over the visible world is the sun and the equivalent in the intelligible world is the Good (Johnson & Reath, 2007). (In the Cave analogy, the fire is the sun and the sun the Good). The line is divided across to reveal different stages resulting in four levels altogether horizontally and eight stages vertically (four on each side). The bottom four stages are referred to as “A, B, C, and D” (see Figure 1). As one ascends these stages on the chart, (bottom to top); it represents an increase in clarity of understanding (ibid).

“A” represents shadows and reflections, like those seen on the cave wall; “B” represents the objects themselves that can be physically manipulated. This section also includes persons, animals, man-made things, plants etc. Moving from the material realm over to the intelligible realm, “C” represents deductive reasoning or hypothetical postulation. Assumptions are used in drawing conclusions at this stage (Johnson & Reath, 2007). “D” represents studying literature and drawing conclusions from ‘higher’ principles. Here, hypotheses can be used as “spring boards” to ‘higher’ understanding and reasoning which is the next level of clarity (Balashov, 1994, p. 2). In the next level of clarity, science and mathematical principles are utilized in the material world’s ‘equivalent.’ Mathematics and manipulation of its symbols and numbers is the physical representation for the higher equations which represent the Forms. These equations, however, are not completely understood or synthesized, just utilized (Johnson & Reath, 2007). Level; “C” is the secular mathematics that is taught in grade school and high school that only manipulate the numbers without understanding them in their larger context. The assumptions are carried over to the university level.

The ‘highest’ level of the material realm is referred to as ‘Being’ and it represents seeing the world as it really is, and not how it is taught. Realizing this, one can move to the ‘highest’ Good or level of intelligence. This is where dialectical reasoning can be utilized and where the ‘Forms’ or guiding principles behind all physical objects can be understood or even synthesized.

            Plato believes that behind everything in the universe lie mathematical principles, these he refers to as ‘Forms’ (Personal communication C. Hayes, October 2010; Aczel, 2000; Sheldrake, 1988). The Forms are geometric shapes that make up objects in the world around us. There is a whole branch of mathematics called Sacred Geometry or Sacred Mathematics that studies shapes and forms that can be traced back to Pythagoras. “Both Pythagoras and Plato suggested that all citizens learn the properties of the first ten numbers as a form of moral instruction” (Schneider, 1994, p. xxiii). The basic shapes that make up what are now called Platonic solids, were revered so highly that it can be difficult to separate the math from the religion (Aczel, 2000).

Pythagoras (571 BCE) developed a school of mathematics at Crotona that studied sacred geometry as a form of religion. The school’s motto was “God is number” (Aczel, 2000, p. 19). “And by number they meant whole numbers and their ratios” (Aczel, 2000, p. 19). Pythagoras believed that numbers represented God in pattern, symmetry and infinity. When his school discovered irrational numbers it was a threat to their religious beliefs about mathematics because how could God not be perfect and symmetrical. Irrational numbers include numbers with decimals having no intelligible pattern (Aczel, 200, p. 18). For example, “[w]hen the Pythagorean formula is applied to a triangle with two sides equal to one, the result is that the hypotenuse is given by the equation c² = 1² + 1² = 2, so that c = √2” (Aczel, 2000, p. 18). The existence of these numbers seemed to say that God is imperfect, so they kept the discovery of irrational numbers a secret. When Hippasus told the world the secret of the existence of irrational numbers, Greek geometry was born and Pythagoras’ idea of divinity in numbers died (Aczel, 2000). Plato was born in Greece about 100 years later.

The belief that behind everything is a mathematical equation, however, remains strong today. Einstein’s famous E=mc² is evidence to the truth in this statement. Some mathematicians have tried to tie all the different mathematical principles into one all encompassing principle called the Grand Unified Theory (Einstein, 1956) or the Unified Field Theory (Hawking, 1988). This journey is similar to those who try to construct Plato’s Divided Line mathematically. This is not an exhaustive list, but many problems arise when it is attempted and most say it cannot be done (Personal communication C. Hayes, October 2010). For example, the subsections A and B relate to their equivalent sections in the intelligible realm (C and D) in a ratio that equals A + B (Balashov, 1994). Therefore, A + B = C + D or A/B = C/D (Personal communication C. Hayes, October 2010). This relationship can also be interchanged showing that B = C (Balashov, 1994).  But, this is where the conundrum begins because Plato says that as one ascends, clarity increases. This implies ontological superiority as one climbs up the Line. He also states that the intelligible realm is superior to the material realm. Therefore, how can A, B, C and D be equal to one another if ontological superiority is implied? I propose that there is a movement towards a more complete state, but it does not necessarily travel up or down or left to right. When this state is reached, the journey then becomes to remain there and hold your ground despite of the resistance and despite of those who want to throw you off or out of this intellectual space. This will be addressed in more detail further on in the paper.  

The feud of rational versus irrational numbers comes back into play here because another problem with plotting the Divided Line is that it is unclear whether rational or irrational numbers should be used in its construction. Perhaps irrational numbers are to be used when constructing the Divided Line mathematically. This brings us back to the “problem of the irrational” because when using irrational numbers, they cannot be represented by one number (Benjafield, 2005, p. 6). Using an irrational number will therefore produce an answer that is always slightly off because it cannot be calculated or manipulated without rounding. However, the school of Pythagoras was represented by the symbol of the five-pointed star within a pentagon which is inset with another five-pointed star within a pentagon and so on. What is curious about this symbol is that it represents phi or the golden ratio, which is an irrational number (Aczel, 2000). If the Pythagoreans wanted to keep the existence of irrational numbers a secret, why promote them by having one as their symbol? I find it interesting that an irrational number cannot be expressed by one number but can be expressed in one symbol. This symbol or pattern does an excellent job of summing up the ratio in one, elegant and simple design. I propose that Plato’s Divided Line is not a line in the linear sense, but rather a pattern; that of a spiral. This is why it is difficult to plot the Line and why the proportions cannot be derived properly. This is also why the idea of ontology is so difficult to comprehend within it. For example, when transforming a map of the world from a three dimensional format to a two dimensional surface, the proportions change and you end up with a map looking like the one in Figure 2 called the Homolosine (Goode, 1925). Thinking of the Line as a spiral or a pattern could be a step closer to actually plotting it.

By stating that the Line is not a linear line, but rather a pattern or a spiral aids in solving the conundrum of the Divided Line because this way the boxes can create a movement along, as well as unfold on an equal plane, thus addressing the problem of ontology. Due to binaristic thinking, we tend to think of things in a linear fashion or hierarchy, when in reality, the relationship is neutral. As one travels along the spiral, it seems as though you are making progress towards something; thus ascension is assumed. Our experience of the physical world is such; we think we are travelling in a straight line, yet we are really following the geodesics of the spherical earth and can eventually end up where one began. This is why when some refer to it as the “highest” Good, it is misleading and throws off calculations of those trying to plot because it makes one think it should be plotted linearly.    

Reaching the Good

The Golden Ratio or Golden Section would be the most appropriate irrational number to use when plotting the Line. The Golden Section is represented by the equation: phi equals the square root of five plus one over two (Balashov, 1994). This equals roughly 1.618, which is an irrational number because it displays no pattern as it repeats into infinity (much like pi). Using this equation or number, the line would be divided in two and the proportion of the smaller section would be to the larger section as the larger to the entire line. Therefore, “the smaller is to the larger as the larger is to the whole” (Benjafied, 2005, p. 6). This makes a beautiful, aesthetic proportion that is found in the body and face (1:1.618). For example, the ratio of the width of the mouth to the width of the nose is proportionate to the distance between the navel and foot to the height of the person. This Golden Section can be found all over in nature and in art (Aczel, 2000; Benjafied, 2005). But, the problem in using this ratio is that it is not known how long the Divided Line is supposed to be and it is therefore impossible to know the true proportions of the sections. However, by turning the line into a spiral, of similar proportions to phi, it could be said that the proportions of the boxes need not be determined by the size or length of the line. The ‘line’ would spiral off into infinity, leaving the proportions as they are, no matter how long the Line.

 The Mandelbrot Set or Fractal equation works in a similar manner. On one side of the equation, it spirals out and on the other; it spirals in (Clarke, 1994). When browsing through the Fractal equation, it does not matter how far you go into it (or for how long), the patterns keep coming. The quality or proportions of the next fractal are not lost, no matter how far you can humanly go. Therefore, the length is irrelevant to the proportions. Placing a limit on the unlimited would lead to skewed calculations.

The Fractal also does not follow a straight line or path. Therefore, it could not be said that one way of travelling through the equation is better than another, so this does not promote ontological distinctions. However, for the Fractal, it does not matter how long the path of trajectory, the proportions remain the same and work on similar principles to the Golden Ratio (Clarke, 1994). Treating the line as dynamic, rather than static may be the key to understanding the proportions of the Line.   

Another problem emerges when reaching the top or fourth level of the Divided Line (see Figure 1). If you follow the arrows up the line one reaches an impasse. It is not possible to reach the final level directly from beneath. The obstacles create so much counter-friction that trying to reach the ‘highest’ level in a linear fashion becomes impossible. It is like how continuous data can be reduced to a mathematical absurdity. For example, on the number line, if one divides a number in half, then in half again, it can be divided in half infinitely, without ever reaching the destination of the next number (Aczel, 2000). The obstacles, in particular, the ‘puppet people’ work against the person trying to transcend the illusion, and create so much friction and resistance that momentum is lost; making it nearly impossible to reach the fourth level of the Divided Line from the third (directly). Trying to reach Plato’s true Sun outside the cave is much like real attempts to reach the speed of light. For example the mathematical equation that describes this is: half times mass times velocity squared (see Figure 3). Therefore, one could run into a similar problem when trying to transcend into the intelligible realm. It is just not possible to perceive the ‘highest’ Good directly, much like how matter cannot reach the speed of light. However, due to our tendency to think linearly and in straight lines, our bias has caused an illusionary problem that is not in fact there.

Plato’s Line is assumed to move up in a two dimensional space, whereas the traditional number line moves left to right on a horizontal plane where along it, 1<2 etc. This leads us to another obstacle in plotting the Divided Line. It is not clear whether the line should be constructed vertically or horizontally. Some say that because Plato intends the person to ascend, that it should be constructed vertically (Balashov, 1994). To overcome this obstacle I suggest using both by plotting it on all four vertices (a Cartesian Graph). Plotting the Fibonacci sequence onto a grid, your get the Golden Ratio! I hypothesize that if the Golden Section is used to represent the movement along the Line, as suggested above, the answer would be to plot it both horizontally and vertically. When travelling along a spiral, all directions are needed. However, when plotting the Golden Ratio in two dimensions, as opposed to four, it looks more like the bottom of Figure 3. The spiral does not start until one reaches a certain level. Therefore, in two-dimensional thinking and being, there is a sort of ontological progression to reach the spiral; hence the confusion inherent in its ontological construction.   

One ascends vertically through A and C, for westernized convenience, lets begin this ascent on the far left side of Figure 1. Then the progress is horizontal to the other side of the chart. It then proceeds diagonally to the third level’s horizontal line dividing illusion from truth as depicted in Figure 1 (the dotted line). One must then ascend on an arc or curved trajectory around the line of obstacles or puppet people dividing the third and fourth levels (see Figure 3). This trajectory reflects the Phi sequence (Meisner, n.d) or the Golden Section and shows how persons can reach the ‘highest’ Good using the Allegory of the Cave and the Divided Line. Therefore, the ‘highest’ Good cannot be reached directly or strictly in a vertical fashion (as our common experience assumes).

If we would take the 3D Golden Ratio and turn it into a 2D ‘Homolosine-like map’ it would look like the trajectory plotted in Figure 3, as suggested above. It is straight and angled in the material world, yet curved and geodesic in the realm of intelligence and enlightenment. In this way, the ‘highest’ Good can only be reached when persons overcome their two-dimensional thinking habits. Realizing that we tend to think two-dimensionally in a multi-dimensional world, we can become enlightened and realize we are living in an illusion; or at least understand that we live in a world based on misleading assumptions created by teaching and learning habits. If we can also understand that we place static limits on a dynamic world, this could also help shatter the illusion. Therefore, the solution to the problem of the Line is to overcome our linear and binaristic thinking and apply more dimensions. Linear and binaristic thinking is only ultimately useful in a two-dimensional world and this does not accurately describe the world in which we live. Plato may be onto something when he states that we have not been taught properly. 

What Can We Do?

In western culture and in reading the English language, we read left to right. Therefore, we assume all other things progress in this manner. In a way, our patterned thinking resides on a two dimensional plane. Perhaps we need to add more dimensions to our commonly held beliefs. In reading Hebrew, it is read right to left. In Chinese symbols are read not only left to right, but bottom to top. Can we truly say that one way of proceeding is superior to another? No. Transforming the number line into a spiral can aid in the conundrum because as one travels, they end up travelling in all directions indiscriminately. This can lead to new thought patterns and restructuring of the brain (neural plasticity) that can spill over into our social lives to end racism and prejudice (Dovidio, Glick & Rudman, 2005). Not only is there movement from left to right and right to left harmonized, but also the directions of up and down. I like to refer to the directions together as SEWN, rather than NEWS for this reason. Once we realize we are living in an illusion, based on misleading assumptions, we can see the world how is really, truly is; a Grand, Living, Dynamic Fractal (Kroeker, 2009).

Another suggestion is to alter curricula to incorporate all forms of mathematics, rather than limit it to the teaching of only Secular Mathematics which teaches maths for the sole purpose of quantifying and describing. The rote memorization of mathematical formulae as taught in schools (Secular Mathematics) has created a cold, unimaginative and disengaging experience. It is a type of mathematics that states that numbers can only be used to quantify and that quantitative mathematics is the superior way to describe all material phenomena. It is unimaginative and “keeps us dull to the potential wisdom that the familiar counting numbers can teach us” (Schneider, 1994, p. xx). This, in turn, reifies science and places it on a pedestal that may be too high for its earned praise. Mathematics, and as an extension, science is incomplete and therefore based on half truths. It masquerades as an island, when it is not, it needs Philosophy.

The institution of Secular Mathematics and the scientific method has created in persons a reverence of material explanations of the phenomenal world. This, in turn, “causes [us] to create an apparatus of investigation and a set of concepts that produce material explanations, no matter how counter-intuitive to the uninitiated” (Schneider, 1994, p. xx). I argue that Secular Mathematics (SM) and the scientific method are based on an incomplete (therefore misleading) premise and is arbitrary in nature. In order for mathematics and quantitative scientific methodology to be complete, this project suggests a full recognition and understanding of patterns and relationships to be a necessary prerequisite for research design. I propose that a Mixed Methods approach in research would be optimal and that Symbolic Mathematics (relationships and patterns) and Sacred Geometry (Platonic Solids) be added to grade scholl and high school curricula. The end result just may also get girls and women more interested in Math!

            Scientists confirm with formulas what ancient seers knew through revelation;

That the world’s patterns and cycles are harmonious when seen as mathematical

relationships. The ancients’ intuitive revelations were grounded by the study of nature,

 numbers and shapes.  (Schneider, 1994, p. xxv)

This brings us full circle, back to the realm of Philosophy. I hope you enjoyed the journey through Philosophy to Theology to Psychology to Genetics to Gender Studies and Sociology to Mathematics and back. The individual branches of research and topics are also incomplete without each other. I am looking forward to the next General Systems Theory that aims to gather together all departments within a university to a common purpose of Interdisciplinarity. Thank you for your time and I am glad that you gave me the opportunity to shatter the illusion and help you reach the ‘highest’ Good.

Side Note Regarding the Number Line and the Axiom of Choice

            There is one other suggestion regarding the problems inherent within the number line that I did not get to as I am not sure it fits nicely here, but I have a potential solution to another quandary regarding the number line. When manipulating the number line, one is faced with a conundrum that begs the question “what is the line itself made of?”  “How are all the numbers tied together?” No matter how deep you go, there is still a space between each number, no matter how miniscule. I suggest that the glue binding the numbers together on the number line are the number actions, such as +, -, x, /, =, <,>, % , $ etc. The symbols tie the numbers together by guiding or providing direction of how the numbers are to be used. A lot of the time we look at something without considering the actor. This is a problem inherent within Psychology as mentioned above, we seem to forget that we are an acting part of the equation; a variable forever confounded that can never be controlled for properly. This is why I am a firm believer in the axiom of choice.

Adding the axiom of choice creates a world of problems for mathematics because “[t]he method of proof that mathematicians have decided to use requires that results be obtainable by a finite number of steps” (Aczel, 2000, p. 176, italics in original). I am unconvinced that the best way to deal with an infinite number line is to place arbitrary limits onto it. This is why it was so hard to plot the Divided Line, the mathematics depended on how long the Line is because the axioms of mathematics are set up to necessitate limits and turn something infinite into something finite for analysis. (Much like using fixed Earth mathematics to launch rockets out of our atmosphere). A common critique of adding the axiom of choice is there is no guideline telling us where to go and what to do, making it randomized and arbitrary. However, I suggest that using hypotheses as one goes through mathematical procedures can help provide guidelines of where to go and what application to apply.

Another critique of the axiom of choice is that it is assumed if it were applied; the sequential order of the numbers would be ignored.

Consequently, there is no theoretical way to look at these numbers without

considering this property of order, i.e., it makes no sense to try to jumble up

the numbers and consider them as a unordered set. (Aczel, 2000, p. 177)

If, we apply the suggestion above to consider the number line as a spiral, rather than a linear line, this may help solve this conundrum. This does not involve jumbling the numbers out of order, it just involves placing them in an order where they can be seen as a set, or on an equal plane, rather than as individual numbers placed in a hierarchy.       

 

 

 

 

 

 

References

Aczel, A. D. (2000). The Mystery of the Aleph: Mathematics, the Kabbalah, and the Search for

Infinity. New York: Washington Square Press.

Alcoff, L. (1991-1992). The Problem of Speaking for Others. Cultural Critique. 20: 5-32.

Balashov, Y. (1994). Should Plato’s Line be Divided in the Mean and Extreme Ratio. Ancient

            Philosophy 14: 283-295. Web. 18 Feb. 2011.

Benjafield, J. G. (2005). A history of psychology. Second edition. Toronto: Oxford

University Press.

Bourdieu, P. (1986). The forms of capital. In J.E. Richardson (Ed.), Handbook of theory of

research for the sociology of education (pp. 241-258). New York: Greenwood Press.

Clarke, A. (1994). The colors of infinity. Retrieved November, 1998) from

http://www.youtube.com/watch?v=QZA5ZOs_E8s&feature=related

Cornford, F. (1965). The Republic of Plato. New York: Oxford University Press.

Dovidio, J. F., Glick, P., & Rudman, L. A. (2005). On the Nature of Prejudice: Fifty Years After

Allport. Malden MA: Blackwell Publishing.

Einstein, A. (1956). Out of my Later Years. New York: Random House.

Goode, J.P. (1925). The Homolosine projection--a new device for portraying the Earth's surface

entire: Association of American Geographers, Annals, v. 15, p. 119-125.

Harding, S. (2007). Feminist Standpoints. Hesse-Biber, S. Handbook of Feminist Research. Sage

            Publications LTD (UK). Print.

Hawking, S. (1988). A Brief History of Time: From the Big Bang to Black Holes. Toronto:

Bantam Books.

Hendricks, R. G. (1998). (Ed.) Lao-Tzu Te-Tao Ching: A New Translation Based on the Recently

 Discovered Ma-wang-tui Texts. New York: Ballantine Books.

Hibbs, T., Pothier, D. (2005). Post-secondary education and disabled students: Mining a level

playing field or playing in a minefield? In D. Pothier & R. Devlin (Eds.), Critical

disability theory: Essays in philosophy, politics, policy, and law. (p. 195-219). Vancouver: UBC Press.

Jhally, S. (2013). Image-based culture: Advertising and popular culture. In M. Hobbs & C. Rice

(Eds.), Gender and women’s studies in Canada: Critical terrain (pp. 327-335). Toronto:

Women’s Press.

Johnson, O. A., & Reath, A. (2007). Ethics: Selections from classical and contemporary writers.

            Eds. Belmont: Thomson Wadsworth.

Kroeker. S. (2009). The Grand patchwork: A theory in the making. Retrieved from

http:www.thegrandpatchwork.com

Kroeker, S. (2008). The importance of equal validation of rational and intuitive cognitive styles.

            Presented at the first National Undergraduate Psychology Research Conference:

            Kwantlen University College, Richmond British Columbia, Canada.

Lareau, A. (2011). Unequal childhoods. Berkley: University of California Press.

Meisner, G. (n.d). Golden Number.net. N.p., n.d. Web. 25 Feb. 2011

Meyer, M. (2005). The Gnostic Gospels of Jesus: The definitive collection of mystical gospels

 and secret books about Jesus of Nazareth. New York: HarperCollins Publishers Inc.

Narayan, U., Harding, S. (2000). Decentering the Center: Philosophy for a Multicultural,

Postcolonial, and Feminist World. Bloomington: Indiana University Press. Print.

Piff, P. K, Dietze, P., Feinberg, M., Stancato, D.M., Keltner, D. (2015). Awe, the small self and

prococial behaviour. Journal of Personality And Social Psychology. 108 (6), pp. 883-99.

Plumwood, V. (1993).  Feminism and the Mastery of Nature. London: Routledge. Print.

Scarr, S., McCartney, K. (1983). How people make their own environments: A theory of

genotype -à effects. Child Development, 54, 424-435.

Sheldrake, R. (1988). The Presence of the Past: Morphic Resonance and the Habits of Nature.

New York: Vintage Books.

Stan, L. (2009). Either Nothingness or Love: On Alterity in Soren Kierkegaard’s Writings.

 Saarbrucken, Web. 15 Oct. 2010.

St. John, P. (2010). Crossing scripts and swappin riffs: Preschoolers make musical meaning. In

 M.C. Connery, V. P. John-Steiner & A. Marjanovic-Shane (eds.), Vygotsky and

creativity: A cultural-historical approach to play, meaning making, and the arts (pp. 63-

81). New York: Houghton Mifflin Harcourt Publishing Company.

The Wachowskis (Producers). (1999). The Matrix [DVD]

Von Bertalanffy, L. (1972). The history and status of general systems theory. Academy of

Management Journal, 15(4), 407-426.

 

  Figure 1: Plato’s cave allegory juxtaposed to the divided line.

 

 

 

Figure 2:  The Homolosine (Goode) and the pentacle (Pythagoras)

 

 

 
 

 

                                                   

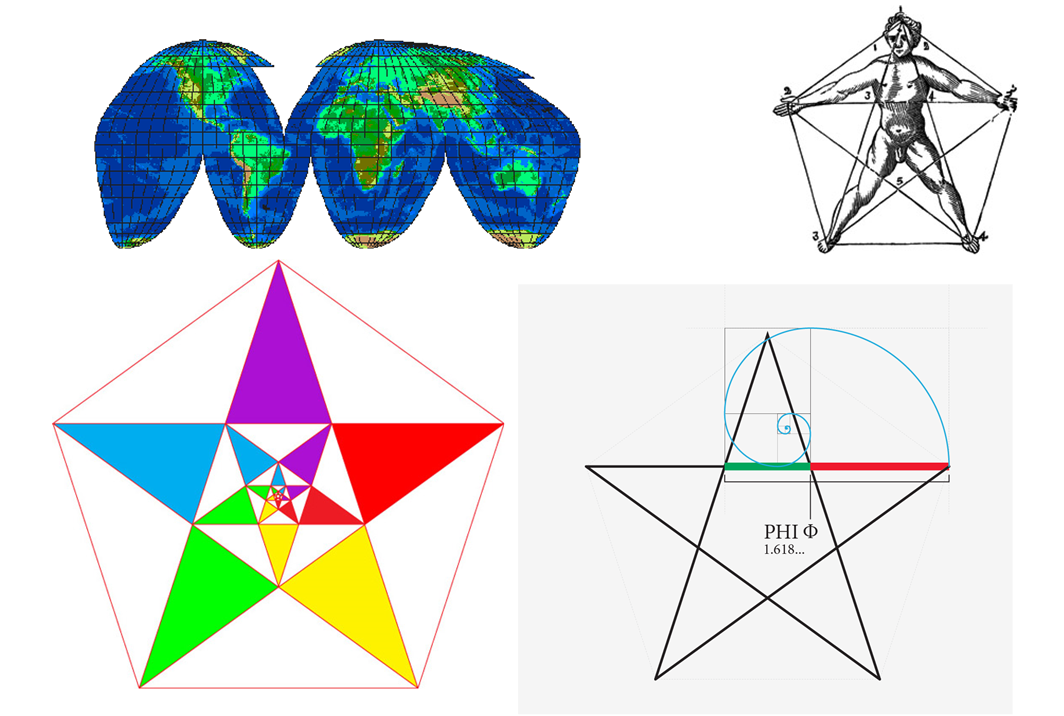
Figure 3: A homolosine-like diagram of the golden spiral and one’s trajectory through the divided line before reaching the spiral (Kroeker).